Péndulos acoplados

Cálculo con diferentes largos y masas¶

Esta es la teoría que hace falta para analizar los datos de los péndulos acoplados.

1. Ecuaciones de movimiento
2. Modos normales
3. Masas iguales, largos diferentes
4. Frecuencias iguales, masas diferentes
5. Conclusiones

1. Ecuaciones de movimiento¶

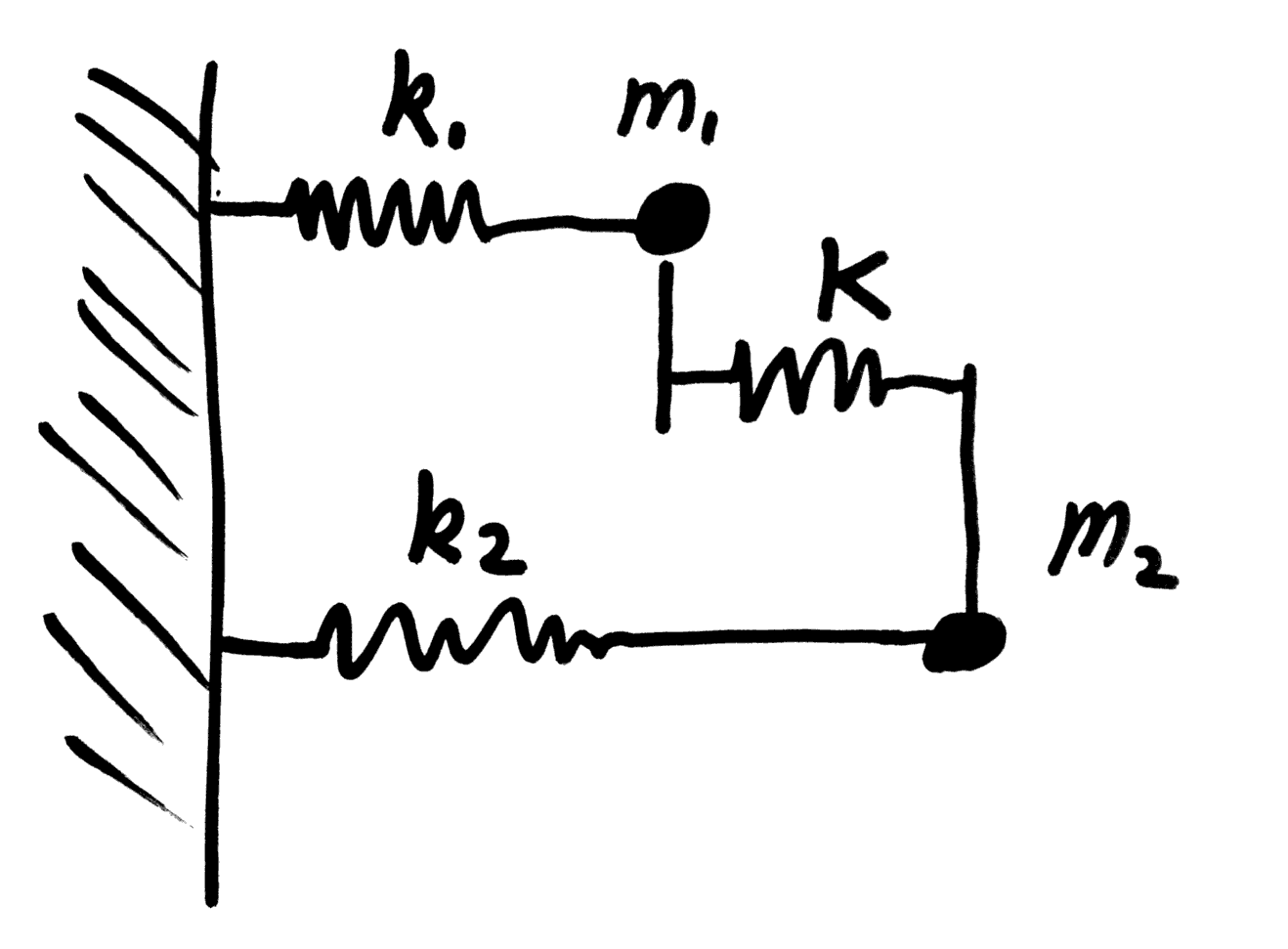
Las ecuaciones de Newton son:

$$ \left\{ \begin{array}{ccc} m_1 \ddot{x_1} &=& - k_1 x_1 - K (x_1-x_2) \\ m_2 \ddot{x_2} &=& - k_2 x_2 - K (x_2-x_1) \end{array} \right. $$

Podemos reordenar los términos para llegar a la expresión:

$$ \left\{ \begin{array}{ccc} \ddot{x_1} + (\omega_1^2+\Omega_1^2)\ x_1 - \Omega_1^2\ x_2 &=& 0 \\ \ddot{x_2} + (\omega_2^2+\Omega_2^2)\ x_2 - \Omega_2^2\ x_1 &=& 0 \end{array} \right. $$

donde:

$\omega_i^2=\frac{k_i}{m_i}$ es la frecuencia de cada péndulo aislado

$\Omega_i^2=\frac{K}{m_i}$ es la magnitud del acople sobre la masa $i$

2. Modos normales¶

Los modos normales de oscilación son aquellos en loa que todas las masas se mueven con la misma fracuencia:

\begin{eqnarray} \left(\begin{array}{c} x_1 \\ x_2 \end{array}\right) &=& \left(\begin{array}{c} a_1 \\ a_2 \end{array}\right)\ e^{i\omega t} \nonumber \\ \ddot{x_n} &=& -\omega^2 \ x_n \nonumber \end{eqnarray}

La ecuación de movimiento de convierte en:

$$ \mathbf{M} \cdot \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) = \mathbf{0} $$

donde:

$$\mathbf{M} = \begin{pmatrix} (\omega_1^2+\Omega_1^2) - \omega^2 && -\Omega_1^2 \\ -\Omega_2^2 && (\omega_2^2+\Omega_2^2) - \omega^2 \end{pmatrix} $$

Las frecuencias de los modos se obtienen planteando la ecuación característica:

$$ \det(\mathbf{M}) = 0 $$

y obtenemos una ecuación de segundo grado en $\omega^2$:

$$ \omega^2_\pm = \frac{\left(\omega_1^2+\Omega_1^2 \right) + \left(\omega_2^2+\Omega_2^2 \right)}{2} \pm \frac{\sqrt{\left[ \left(\omega_1^2+\Omega_1^2 \right) - \left(\omega_2^2+\Omega_2^2 \right) \right]^2 + 4\Omega_1^2 \Omega_2^2}}{2} $$

Los modos normales son oscilaciones caracterizadas por las amplitudes relativas $a_2/a_1$ de cada coordenada.

Son la solución de la ecuación:

$$ M_{11} \ a_1 + M_{12} \ a_2 = 0 $$

En nuestro caso:

$$ q = \frac{a_2}{a_1} = - \left( \frac{ \omega^2 - (\omega_1^2+\Omega_1^2) }{\Omega_1^2} \right) $$

Dos observaciones sobre esto último:

las dos soluciones tienen signos diferentes. La solución con $\omega_+$ da negativa y corresponde a un modo antisimétrico y la $-$ al modo simétrico.
en módulo, $q_+$ es mayor que $q_-$ de manera que $0 < -\frac{q_+}{q_-} < 1$

Cuando esté oscilando según un modo normal, el movimiento tendrá la forma:

$$ \mathbf{x} = A_\pm \ ( 1 \ ;\ q_\pm ) \ e^{i \omega_\pm t} $$

y como las soluciones se pueden superponer, la forma más general de movimiento es

$$ \mathbf{x} = A_+ \ (1 ;\ q_+ ) \ e^{i \omega_+ t} + A_- \ (1 ;\ q_- ) \ e^{i \omega_- t} $$

donde las amplitudes $A_\pm$ son números complejos, pero las posiciones y velocidades son la parte real de estas relaciones.

Supongamos que suelto el péndulo $1$ desde cietra amplitud $A$ mientras el otro está quieto en el equilibrio. En ese caso, la posición inicial implica que:

\begin{eqnarray} \Re (A_+ + A_-) &=& A \nonumber \\ \Re (A_+ q_+\ +\ A_- q_-) &=& 0 \nonumber \end{eqnarray}

mientras que las velocidades iniciales:

\begin{eqnarray} \Im (\omega_+ \ A_+ + \omega_- \ A_-) &=& 0 \nonumber \\ \Im (\omega_+ \ A_+q_+\ +\ \omega_- \ A_- q_-) &=& 0 \nonumber \end{eqnarray}

Estas ecuaciones son complejas, pero las frecuencias y los $q$ son reales. También es real la posición inicial $A$.

Las dos últimas ecuaciones nos dicen que los coeficientes $A_\pm$ son reales y las dos primeras nos dicen que:

\begin{eqnarray} A_+ \ \left( 1-\frac{q_+}{q_-} \right) &=& A \nonumber \\ A_- &=& - \left( \frac{q_+}{q_-} \right) A_+ \nonumber \end{eqnarray}

Por las consideraciones que hicimos sobre $q_\pm$ resulta que ambos $A_\pm$ tienen el mismo signo y además
$A_+ > A_-$ con estas condiciones iniciales.

El péndulo $1$ comienza con amplitud $A$ pero a medida que pasa el tiempo, ambas oscilaciones se van desfasando, hasta llegar a una amplitud mínima que será:

$$ A_{min} = A_+ - A_- = A \ \left( \frac{1+{q_+}/{q_-}}{1-{q_+}/{q_-}} \right) $$

El péndulo $2$ comienza quieto y tiene ambas oscilaciones en contrafase. Luego de un tiempo alcanzará un máximo cuando:

$$ A_{max} = A_+ q_+ - A_- q_- = 2 A_+ q_+ = 2A \ \left( \frac{q_+}{1-{q_+}/{q_-}} \right) $$

y no es imposible ver que

$$ \omega_{mod} = \omega_+ - \omega_- $$

3. Masas iguales, largos diferentes¶

Si las masas son iguales, resulta: $$ \Omega_1^2=\Omega_2^2=\Omega^2$$

$$\omega^2_\pm = \left( \frac{\omega_1^2+\omega_2^2}{2}\right) + \Omega^2 \pm \sqrt{\left( \frac{\omega_1^2-\omega_2^2}{2}\right)^2 + \Omega^4} $$

Para interpretar esta ecuación, conviene expresarla en función de la relación de frecuencias:

$$f = \omega_2/\omega_1$$

y el acoplamiento normalizado por $\omega_1$:

$$\alpha = \Omega/\omega_1$$

Los resultados de las frecuencias y las amplitudes quedan:

$$ \omega^2_\pm = \omega_1^2 \left\{ \ \left( \frac{1+f^2}{2} \right) + \alpha^2 \pm \sqrt{ \left( \frac{1-f^2}{2} \right)^2 + \alpha^4 } \right\} $$

$$ q_\pm = - \frac{1}{\alpha^2} \left\{ \left(\frac{f^2-1}{2}\right) \pm \sqrt{ \left( \frac{f^2-1}{2} \right)^2 + \alpha^4} \right\} $$

In [3]:

def om(f,a):
    uno =       (1+f**2)/2 + a**2
    dos = sqrt(((1-f**2)/2)**2 + a**4)
    return sqrt(uno-dos),sqrt(uno+dos)

def Amin(f,a):
    dif = (f**2-1)/2
    uno = dif/a**2
    dos = sqrt(dif**2 + a**4) / a**2
    qp,qm = -(uno+dos), -(uno-dos)
    qqq = qp/qm
    Am = (1+qqq)/(1-qqq)
    return abs(Am),qp,qm

F=linspace(.8,1.2,101)
A=[.1,.2,.3]
co = ['b','r','g','orange']

figure(figsize=(15,18))
subplot(411)
for i,a in enumerate(A):
    omm,omp = om(F,a)
    plot(F,omm,color=co[i],label=r'$\alpha = {:.1f}$'.format(a), lw=3)
    plot(F,omp,color=co[i] ,  lw=3)

title('Frecuencias propias', fontsize=25)    
#xlabel(r'$\omega_2/\omega_1$',fontsize=25)   
ylabel(r'$\omega_\pm$',fontsize=25)   
ylim(0.8,1.25)
legend(fontsize=15)    
grid()

subplot(412)
for i,a in enumerate(A):
    omm,omp = om(F,a)
    plot(F,omp-omm,color=co[i],label=r'$\alpha = {:.1f}$'.format(a), lw=3)
title(r'Frecuencia de modulación', fontsize=25)    
#xlabel(r'$\omega_2/\omega_1$',fontsize=25)   
ylabel(r'$\omega_{mod}$',fontsize=25)   
legend(fontsize=15)    
grid()

subplot(413)
for i,a in enumerate(A):
    Am,qp,qm = Amin(F,a)
    AM=-2*qp/(1-qp/qm)
    plot(F,Am,color=co[i],label=r'$\alpha = {:.1f}$'.format(a), lw=3)
    plot(F,AM,color=co[i], lw=3)
title(u'Amplitud mínima y máxima', fontsize=25)    
#xlabel(r'$\omega_2/\omega_1$',fontsize=25)   
ylabel(r'$A_{min-max}/A$',fontsize=25)   
legend(fontsize=15)    
grid()

subplot(414)
for i,a in enumerate(A):
    Am,qp,qm = Amin(F,a)
    AM=-2*qp/(1-qp/qm)
    plot(F,qp,color=co[i],label=r'$\alpha = {:.1f}$'.format(a), lw=1.5)
    plot(F,qm,color=co[i], lw=1.5)
title(u'Modos', fontsize=25)    
xlabel(r'$\omega_2/\omega_1$',fontsize=25)   
ylabel(r'$q_+ \ \ q_-$',fontsize=25)   
ylim(-5,5)
legend(fontsize=15)    
grid()

4. Frecuencias iguales, masas diferentes¶

Si las masas son diferentes, pero las frecuencias propias son iguales, resulta: $$ \omega_1^2=\omega_2^2=\omega_0^2$$

$$\left\{ \begin{array}{ccl} \omega^2_+ &=& \omega_0^2 + \Omega_1^2 + \Omega_2^2 \\ \omega^2_- &=& \omega_0^2 \end {array} \right. $$

y si definimos al cociente de las masas: $$ \beta = \frac{m_2}{m_1} $$

$$ \Omega_1^2 + \Omega_2^2 = K\ \left( \frac{1}{m_1} + \frac{1}{m_2} \right) = \Omega_1^2 \ \left( \frac{1+\beta}{\beta} \right) $$$$\left\{ \begin{array}{ccl} q_+ &=& -\frac{1}{\beta^2} \\ q_- &=& 1 \end {array} \right. $$

In [4]:

def of(b,o1):
    if type(b) == float:
        return 1,1 + o1**2 * (1+b)/b
    else:
        return ones(len(b)),1 + o1**2 * (1+b)/b

def Afmin(b,o1):
    if type(b) == float:
        qp,qm = -1/b**2, 1
    else:
        qp,qm = -1/b**2, ones(len(b))
    qqq = qp/qm
    Am = (1+qqq)/(1-qqq)
    return abs(Am),qp,qm

B =linspace(.5,1.6,101)
Om=[.1,.2,.3]
co = ['b','r','g','orange']

figure(figsize=(15,18))
subplot(411)
for i,a in enumerate(Om):
    omm,omp = of(B,a)
    plot(B,omm,color=co[i], lw=len(Om)-(2*i-2))
    plot(B,omp,color=co[i],label=r'$\alpha = {:.1f}$'.format(a) ,  lw=3)

title('Frecuencias propias', fontsize=25)    
ylabel(r'$\omega_\pm$',fontsize=25)   
ylim(0.95,1.25)
legend(fontsize=15)    
grid()

subplot(412)
for i,a in enumerate(Om):
    omm,omp = om(B,a)
    plot(B,omp-omm,color=co[i],label=r'$\alpha = {:.1f}$'.format(a), lw=3)
title(r'Frecuencia de modulación', fontsize=25)    
ylabel(r'$\omega_{mod}$',fontsize=25)   
ylim(0,0.5)
legend(fontsize=15)    
grid()

subplot(413)
for i,a in enumerate(A):
    Am,qp,qm = Afmin(B,a)
    AM=-2*qp/(1-qp/qm)
    plot(B,Am,color=co[i],label=r'$\alpha = {:.1f}$'.format(a), lw=2*len(Om)-(2*i-2))
    plot(B,AM,color=co[i], lw=2*len(Om)-(2*i-2))
title(u'Amplitud mínima y máxima', fontsize=25)    
ylabel(r'$A_{min-max}/A$',fontsize=25)   
legend(fontsize=15)    
grid()

subplot(414)
for i,a in enumerate(A):
    Am,qp,qm = Afmin(B,a)
    AM=-2*qp/(1-qp/qm)
    plot(B,qp,color=co[i],label=r'$\alpha = {:.1f}$'.format(a), lw=2*len(Om)-(2*i-2))
    plot(B,qm,color=co[i], lw=2*len(Om)-(2*i-2))
title(u'Modos', fontsize=25)    
xlabel(r'$m_2/m_1$',fontsize=25)   
ylabel(r'$q_+ \ \ q_-$',fontsize=25)   
ylim(-5,5)
legend(fontsize=15)    
grid()

5. Conclusiones¶

No las agrego deliberadamente para recibir sugerencias y porque no es la idea de este apunte, que sólo pretende tener a mano las cuentas básicas.

Intereses Eclécticos

Curiosidad documentada